Spark 之 Graphx

更新于: | 分类于 |
字数统计: 4.3k 字 | 阅读时长 ≈ 19 分钟

Spark 之 Graphx

1. Graphx 概述

1.1 什么是 Graphx

![image_1cmv2t6351udeheo17feif818sgm.png-77.5kB][1]

Spark GraphX是一个并行图计算框架，它是基于Spark平台提供对图计算和图挖掘简洁易用的而丰富的接口，极大的方便了对饼形图处理的需求。那么什么是图，都计算些什么？众所周知社交网络中人与人之间有很多关系链，例如Twitter、Facebook、微博和微信等，数据中出现网状结构关系都需要图计算。

GraphX是一个新的Spark API，它用于图和并行图(graph-parallel)的计算。GraphX通过引入弹性分布式属性图（Resilient Distributed Property Graph）： 顶点和边均有属性的有向多重图，来扩展Spark RDD。为了支持图计算，GraphX开发了一组基本的功能操作以及一个优化过的Pregel API。另外，GraphX也包含了一个快速增长的图算法和图builders的集合，用以简化图分析任务。

从社交网络到语言建模，不断增长的数据规模以及图形数据的重要性已经推动了许多新的分布式图系统的发展。 通过限制计算类型以及引入新的技术来切分和分配图，这些系统可以高效地执行复杂的图形算法，比一般的分布式数据计算（data-parallel，如spark、MapReduce）快很多。

![image_1cmv2i1fs13e9bi1sftrs919bg9.png-149kB][2]

1.2 Graphx 的特点

灵活性高
![image_1cmv30vj68jrssb1c9m27term1j.png-95.1kB][3]
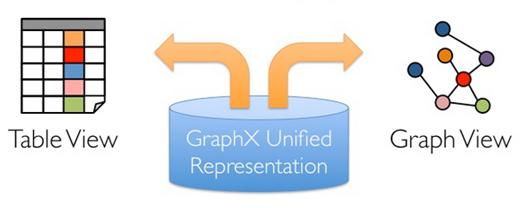
图可以和集合进行无缝对接
GraphX统一了单个系统中的ETL、探索性分析和迭代图计算。您可以查看与图形和集合相同的数据，有效地使用RDD 转换和图的连接操作，以及使用 Pregel API 编写自定义迭代图算法
速度快
![image_1cmv35mns1gdo1sei1jvk16uceac20.png-86kB][4]
可以与最快的专业图形处理系统相媲美。
GraphX与最快的图形系统竞争性能，同时保留Spark的灵活性，容错性和易用性。
算法多
![image_1cmv39mjn186e1nu61fdv1vt1luf2d.png-66.5kB][5]
从不断增加的图算法库中进行选择。
除了高度灵活的API之外，GraphX还提供了各种图形算法，其中许多都是由我们的用户提供的。网页排名，连接组件，标签传播，SVD ++，强大的连接组件以及三角计数等

1.3 学什么

本章主要学习图如何构建，如何计算图，如何应用

1.4 关键抽象

![image_1cmv3h2369kt12m51jtilon1ro52q.png-36.5kB][6]

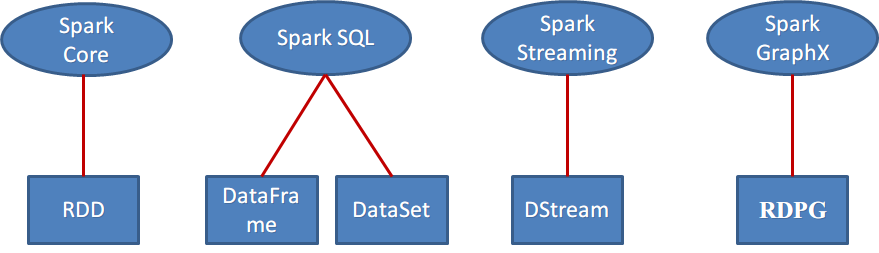
RDPG： Resilient Distributed Property Graph（弹性分布式属性图）

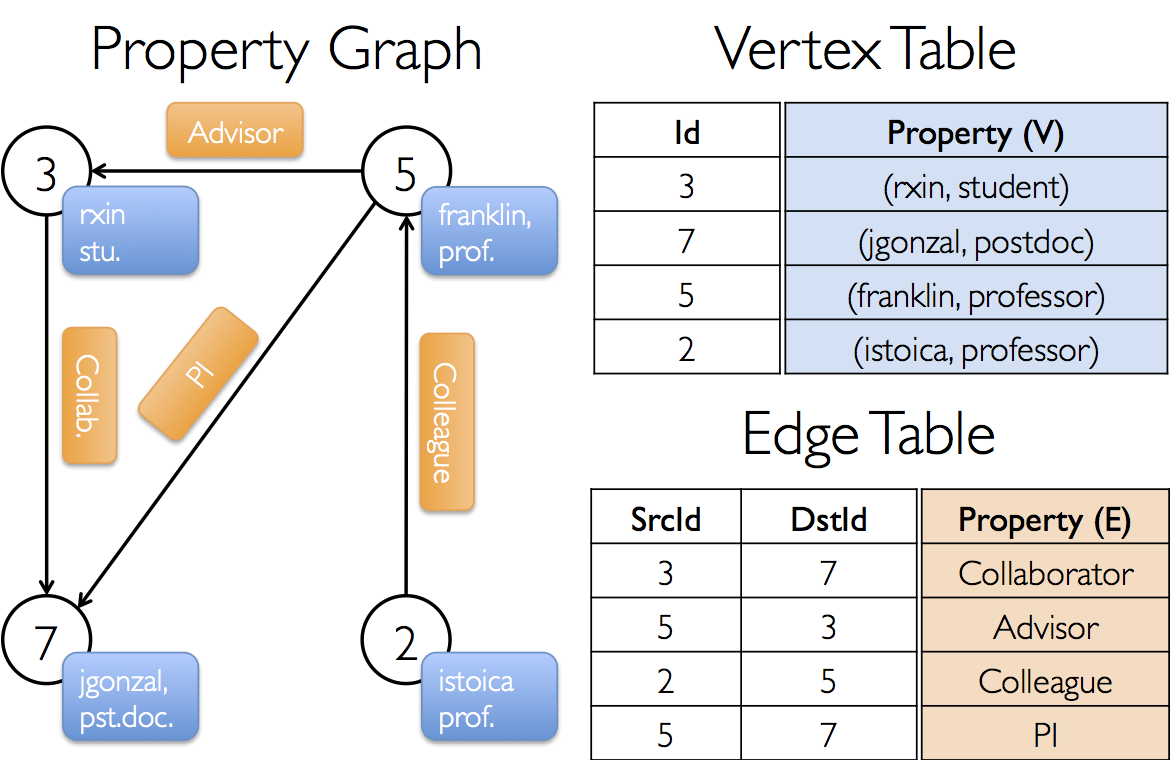
GraphX的核心抽象是弹性分布式属性图，它是一个有向多重图，带有连接到每个顶点和边的用户定义的对象。 有向多重图中多个并行的边共享相同的源和目的顶点。支持并行边的能力简化了建模场景，相同的顶点可能存在多种关系(例如co-worker和friend)。 每个顶点用一个唯一的64位长的标识符（VertexID）作为key。GraphX并没有对顶点标识强加任何排序。同样，边拥有相应的源和目的顶点标识符。
![image_1cmv3u1as1pbqv9jgrqv6trfj3k.png-91kB][7]

相关概念
:

  • 顶点
    RDD[(VertexId, VD)] 表示顶点。

    • VertexId 就是Long类型，表示顶点的ID【主键】。
    • VD表示类型参数，可以是任意类型, 表示的是该顶点的属性。

    VertexRDD[VD] 继承了RDD[(VertexId, VD)]， 他是顶点的另外一种表示方式，在内部的计算上提供了很多的优化还有一些更高级的API。

  • 边 RDD[Edge[VD]] 表示边， Edge中有三个东西：

    • srcId表示 源顶点的ID，

    • dstId表示的是目标顶点的ID，

    • attr表示表的属性，属性的类型是VD类型，VD是一个类型参数，可以是任意类型。

      EdgeRDD[ED] 继承了 RDD[Edge[ED]] ,他是边的另外一种表示方式，在内部的计算上提供您改了很多的优化还有一些更高级的API。
      ![image_1cmv4s5hm1co815181ijg2qg1t0h41.png-216.7kB][8]

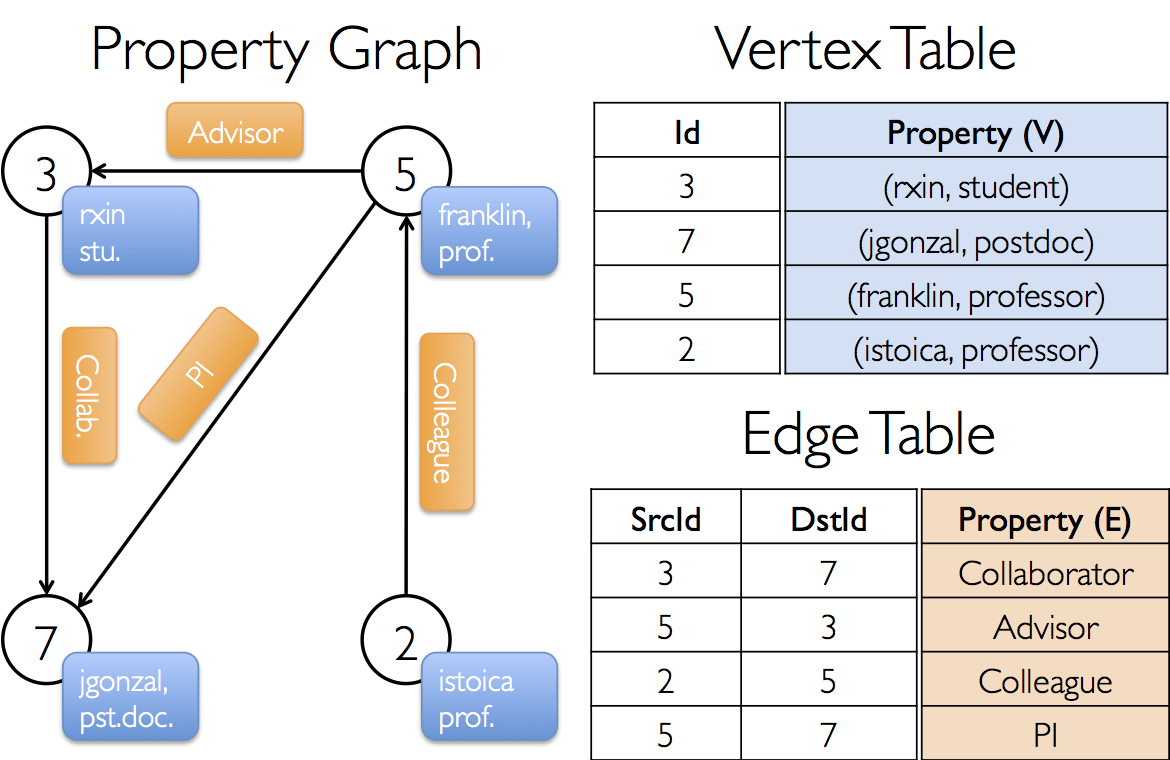
  • 三元组
    EdgeTriplet[VD, ED] extends Edge[ED] 他表示一个三元组， 比边多了两个顶点的属性。包含以下内容srcId、srcAttr、 attr、 dstid、dstAttr
    ![image_1cmv52otn11c3g1v1uecte21qgk4e.png-30.5kB][9]

  • 图 Graph[VD: ClassTag, ED: ClassTag] VD 是顶点的属性、 ED是边的属性

2. 简单案例

2.1 创建一个图

目标
![image_1cmv5rcf6g27obk1rvkd0ko8a4r.png-216.7kB][10]
将上述图中的顶点和边输入到一个图中
添加依赖
1
2
3
4
5
<dependency>
     <groupId>org.apache.spark</groupId>
     <artifactId>spark-graphx_2.11</artifactId>
     <version>${spark.version}</version>
 </dependency>
代码详情
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
package com.zhiyou100.spark

import org.apache.spark.graphx.{Edge, Graph, VertexId}
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext, graphx}

object GraphxHelloWorld extends App{

  //配置对象
  val conf = new SparkConf().setAppName("graphx").setMaster("local[3]")

  //创建sc对象
  val sc = new SparkContext(conf)

  //创建顶点数据集
  val vertexRDD:RDD[(VertexId,(String,String))] = sc.makeRDD(Array(
    (3L,("zhangsan","student")),
    (7L,("wangchen","博士后")),
    (5L,("zhangyu","教授")),
    (2L,("wangguo","教授"))
  ))
  //创建边的数据
  val edgesRDD:RDD[Edge[String]] = sc.makeRDD(Array(
    Edge(3L,7L,"合作者"),
    Edge(5L,3L,"指导"),
    Edge(2L,5L,"同事"),
    Edge(5L,7L,"同事")
  ))

  //构建一个图
  val graphx = Graph(vertexRDD,edgesRDD)

  //RDD展示
  val result = graphx.triplets.collect()

  result.foreach( triplet =>
    println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} ")
  )




  sc.stop()



}

3. 创建

3.1 def apply[VD: ClassTag, ED: ClassTag]

3.2 根据边构建图

根据边直接创建， 所有顶点的属性都一样为 defaultValue

def fromEdges[VD: ClassTag, ED: ClassTag]

1
2


3.3 根据边的两个顶点数据构建

根据裸边来进行创建，顶点的属性是 defaultValue ，边的属性为1

def fromEdgeTuples[VD: ClassTag]

1
2


4. 计算模式

4.1 基本信息

获取边的数量
val numEdges: Long
获取顶点的数量
val numVertices: Long
获取所有顶点的入度
val inDegrees: VertexRDD[Int]
获取所有顶点的出度
val outDegrees: VertexRDD[Int]
获取所有顶点入度与出度之和
val degrees: VertexRDD[Int]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
scala> graphx.numEdges
res0: Long = 4                                                                  

scala> graphx.numVertices
res1: Long = 4                                                                  

scala> graphx.inDegrees
res2: org.apache.spark.graphx.VertexRDD[Int] = VertexRDDImpl[19] at RDD at VertexRDD.scala:57

scala> graphx.inDegrees.collect
res3: Array[(org.apache.spark.graphx.VertexId, Int)] = Array((3,1), (7,2), (5,1))

scala> graphx.outDegrees.collect
res4: Array[(org.apache.spark.graphx.VertexId, Int)] = Array((3,1), (5,2), (2,1))

scala> graphx.degrees.collect
res5: Array[(org.apache.spark.graphx.VertexId, Int)] = Array((3,2), (7,2), (5,3), (2,1))

scala> graphx.edges.collect
res6: Array[org.apache.spark.graphx.Edge[String]] = Array(Edge(3,7,合作者), Edge(5,3,指导), Edge(2,5,同事), Edge(5,7,同事))

scala> graphx.vertices.collect
res7: Array[(org.apache.spark.graphx.VertexId, (String, String))] = Array((3,(zhangsan,student)), (7,(wangchen,博士后)), (5,(zhangyu,教授)), (2,(wangguo,教授)))

scala> graphx.triplets.collect
res8: Array[org.apache.spark.graphx.EdgeTriplet[(String, String),String]] = Array(((3,(zhangsan,student)),(7,(wangchen,博士后)),合作者), ((5,(zhangyu,教授)),(3,(zhangsan,student)),指导), ((2,(wangguo,教授)),(5,(zhangyu,教授)),同事), ((5,(zhangyu,教授)),(7,(wangchen,博士后)),同事))

4.2 转换操作

GraphX中的转换操作主要有mapVertices,mapEdges和mapTriplets三个，它们在Graph文件中定义，在GraphImpl文件中实现。下面分别介绍这三个方法。

4.2.1 mapVertices

mapVertices用来更新顶点属性。从图的构建那章我们知道，顶点属性保存在边分区中，所以我们需要改变的是边分区中的属性。对图中的每一个顶点进行map操作，顶点的ID不能改变，可以将顶点的属性改变成另外一种类型。

4.2.2 mapEdges

def mapEdges[ED2: ClassTag](map: Edge[ED] => ED2): Graph[VD, ED2]

对图中的每一个边进行map操作， 边的方向不能改变，可以将边的属性改变为另外一种类型

4.2.3 mapTriplets

函数定义 函数名 [传入的泛型] （参数：函数（被调用者每一个元素为EdgeTriplet，也就是说这里面的函数的参数就是这种的类型的，拿到这个参数后做什么事都无所谓，但是要保证这个函数返回为ED2））
def mapTriplets[ED2: ClassTag](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]

对于图中的每一个三元组进行map操作， 只能修改边的属性。

4.3 结构操作

4.3.1 reverse

reverse操作返回一个新的图，这个图的边的方向都是反转的。例如，这个操作可以用来计算反转的PageRank。因为反转操作没有修改顶点或者边的属性或者改变边的数量，所以我们可以 在不移动或者复制数据的情况下有效地实现它。
def reverse: Graph[VD, ED]

1
2
3
4
5
6
7
8
9
10
11
scala> graphx.mapVertices((id,attr)=>attr._1+":"+attr._2).triplets.collect.foreach(triplet => println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} "))
srcId=3 srcAttr=zhangsan:student--edge=合作者--dstId=7 dstAttr=wangchen:博士后 
srcId=5 srcAttr=zhangyu:教授--edge=指导--dstId=3 dstAttr=zhangsan:student 
srcId=2 srcAttr=wangguo:教授--edge=同事--dstId=5 dstAttr=zhangyu:教授 
srcId=5 srcAttr=zhangyu:教授--edge=同事--dstId=7 dstAttr=wangchen:博士后 

scala> graphx.mapVertices((id,attr)=>attr._1+":"+attr._2).reverse.triplets.collect.foreach(triplet => println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} "))
srcId=7 srcAttr=wangchen:博士后--edge=合作者--dstId=3 dstAttr=zhangsan:student 
srcId=3 srcAttr=zhangsan:student--edge=指导--dstId=5 dstAttr=zhangyu:教授 
srcId=5 srcAttr=zhangyu:教授--edge=同事--dstId=2 dstAttr=wangguo:教授 
srcId=7 srcAttr=wangchen:博士后--edge=同事--dstId=5 dstAttr=zhangyu:教授

4.3.2 subgraph

subgraph操作利用顶点和边的判断式（predicates），返回的图仅仅包含满足顶点判断式的顶点、满足边判断式的边以及满足顶点判断式的triple。subgraph操作可以用于很多场景，如获取 感兴趣的顶点和边组成的图或者获取清除断开连接后的图。
def subgraph( epred: EdgeTriplet[VD, ED] => Boolean = (x => true), vpred: (VertexId, VD) => Boolean = ((v, d) => true)) : Graph[VD, ED] 

1
2
3
4
5
6
7
8
9
scala> graphx.subgraph(x=>if(x.attr=="同事") true else false,(a,b)=>true).triplets.collect.foreach(tripl => println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} "))
srcId=2 srcAttr=(wangguo,教授)--edge=同事--dstId=5 dstAttr=(zhangyu,教授) 
srcId=5 srcAttr=(zhangyu,教授)--edge=同事--dstId=7 dstAttr=(wangchen,博士后) 

scala> graphx.vertices.collect
res19: Array[(org.apache.spark.graphx.VertexId, (String, String))] = Array((3,(zhangsan,student)), (7,(wangchen,博士后)), (5,(zhangyu,教授)), (2,(wangguo,教授)))

scala> graphx.subgraph(x=>if(x.attr=="同事") true else false,(a,b)=>true).vertices.collect
res20: Array[(org.apache.spark.graphx.VertexId, (String, String))] = Array((3,(zhangsan,student)), (7,(wangchen,博士后)), (5,(zhangyu,教授)), (2,(wangguo,教授)))

4.3.3 mask

mask操作构造一个子图，类似于交集，这个子图包含输入图中包含的顶点和边。它的实现很简单，顶点和边均做inner join操作即可。这个操作可以和subgraph操作相结合，基于另外一个相关图的特征去约束一个图。只使用ID进行对比，不对比属性。
def mask[VD2: ClassTag, ED2: ClassTag](other:Graph[VD2, ED2]): Graph[VD, ED] 

1
2
3
4
5

scala> graphx.mask(graphx1).triplets.collect.foreach(triplet => println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} "))
srcId=3 srcAttr=(zhangsan,student)--edge=合作者--dstId=7 dstAttr=(wangchen,博士后) 
srcId=5 srcAttr=(zhangyu,教授)--edge=指导--dstId=3 dstAttr=(zhangsan,student) 
srcId=5 srcAttr=(zhangyu,教授)--edge=同事--dstId=7 dstAttr=(wangchen,博士后)

4.3.4 groupEdges

groupEdges操作合并多重图中的并行边(如顶点对之间重复的边)，并传入一个函数来合并两个边的属性。在大量的应用程序中，并行的边可以合并（它们的权重合并）为一条边从而降低图的大小。（两个边需要在一个分区内部才行）。合并两条边，通过函数合并边的属性。 【注意】两条边要在一个分区中
def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED]

1
2
3
4
5
6
7
8
9
10
11
12
scala> graphx2.groupEdges((e1,e2)=>e1+e2).triplets.collect.foreach(triplet => println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} "))
srcId=3 srcAttr=(zhangsan,student)--edge=合作者--dstId=7 dstAttr=(wangchen,博士后) 
srcId=2 srcAttr=(wangguo,教授)--edge=同事--dstId=5 dstAttr=(zhangyu,教授) 
srcId=5 srcAttr=(zhangyu,教授)--edge=指导--dstId=3 dstAttr=(zhangsan,student) 
srcId=5 srcAttr=(zhangyu,教授)--edge=同事表兄弟--dstId=7 dstAttr=(wangchen,博士后) 

scala> graphx2.triplets.collect.foreach(triplet => println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} "))
srcId=3 srcAttr=(zhangsan,student)--edge=合作者--dstId=7 dstAttr=(wangchen,博士后) 
srcId=2 srcAttr=(wangguo,教授)--edge=同事--dstId=5 dstAttr=(zhangyu,教授) 
srcId=5 srcAttr=(zhangyu,教授)--edge=指导--dstId=3 dstAttr=(zhangsan,student) 
srcId=5 srcAttr=(zhangyu,教授)--edge=同事--dstId=7 dstAttr=(wangchen,博士后) 
srcId=5 srcAttr=(zhangyu,教授)--edge=表兄弟--dstId=7 dstAttr=(wangchen,博士后)

4.4 聚合

4.4.1 collectNeighbors

该方法的作用是收集每个顶点的邻居顶点的顶点id和顶点属性。需要指定方向
EdgeDirection.out：出的方向
EdgeDirection.in:入的方向
EdgeDirection.Either：入边或出边
EdgeDirection.Both：入边且出边

def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexId, VD)]] 收集邻居节点的数据，根据指定的方向。返回的数据为RDD[(VertexId, Array[(VertexId, VD)])]

1
2
scala> graphx.collectNeighbors(EdgeDirection.Either).collect
res29: Array[(org.apache.spark.graphx.VertexId, Array[(org.apache.spark.graphx.VertexId, (String, String))])] = Array((3,Array((5,(zhangyu,教授)), (7,(wangchen,博士后)))), (7,Array((5,(zhangyu,教授)), (3,(zhangsan,student)))), (5,Array((2,(wangguo,教授)), (7,(wangchen,博士后)), (3,(zhangsan,student)))), (2,Array((5,(zhangyu,教授)))))

4.4.2 collectNeighborIds

该方法的作用是收集每个顶点的邻居顶点的顶点id。它的实现和collectNeighbors非常相同。需要指定方向

def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]

4.4.3 aggregateMessages

def aggregateMessages[A: ClassTag]( sendMsg: EdgeContext[VD, ED, A] => Unit, mergeMsg: (A, A) => A, tripletFields: TripletFields = TripletFields.All) : VertexRDD[A]

每一个边都会通过sendMsg 发送一个消息，

每一个顶点都会通过mergeMsg 来处理所有他收到的消息。

TripletFields存在主要用于定制 EdgeContext 对象中的属性的值是否存在，为了减少数据通信量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
val vertexRDD3 = sc.makeRDD(Array(
    (1L,("zhang1",25)),
    (2L,("zhang2",18)),
    (3L,("zhang3",45)),
    (4L,("zhang4",20)),
    (5L,("zhang5",70)),
    (6L,("zhang6",79)),
    (7L,("zhang7",101))

  ))

  val edgesRDD3=sc.makeRDD(Array(
    Edge(1L,2L,"1"),
    Edge(3L,2L,"1"),
    Edge(1L,4L,"1"),
    Edge(7L,2L,"1"),
    Edge(3L,5L,"1"),
    Edge(7L,6L,"1"),
    Edge(6L,4L,"1")
  ))

  val graph3 = Graph(vertexRDD3,edgesRDD3)
  /*
  aggregateMessages[A: ClassTag](
        sendMsg: EdgeContext[VD, ED, A] => Unit,
        mergeMsg: (A, A) => A,
     )
   */
  graph3.aggregateMessages[Int](
    //发送消息:Map阶段
    triplet=>{
      //将追求者的年龄发送给被追求者
      triplet.sendToDst(triplet.srcAttr._2)
      //triplet.sendToSrc(triplet.dstAttr._2)
    }
    ,//Reduce
    (a,b)=>math.max(a,b)
  )

4.5 关联操作

4.5.1 joinVertices

def joinVertices[U: ClassTag](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD) : Graph[VD, ED]

将相同顶点ID的数据进行加权,将U这种类型的数据加入到 VD这种类型的数据上，但是不能修改VD的类型。

4.5.2 outerJoinVertices

def outerJoinVertices[U: ClassTag, VD2: ClassTag](other: RDD[(VertexId, U)]) (mapFunc: (VertexId, VD, Option[U]) => VD2)(implicit eq: VD =:= VD2 = null) : Graph[VD2, ED]

和joinVertices类似。，只不过是如果没有相对应的节点，那么join的值默认为None。

4.6 Pregel

4.6.1 计算模型

1
2
3
4
5
6
7
8
def pregel[A: ClassTag]
     (
      initialMsg: A,//图初始化的时候，开始模型计算的时候，所有节点都会收到的一个默认的消息
      maxIterations: Int = Int.MaxValue,//最大的迭代次数
      activeDirection: EdgeDirection = EdgeDirection.Either)//发送消息的方向
     (vprog: (VertexId, VD, A) => VD,//节点调用该消息将聚合后的数据和本节点进行属性的合并
      sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],//激活态的节点调用这个方法发送消息
      mergeMsg: (A, A) => A)//如果一个节点收到多条消息，那么就会使用mergeMsg将消息合并为一条消息，如果只接收到一条消息，则不合并

4.6.2 最短路计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
package com.zhiyou100.spark

import org.apache.spark.graphx.{Edge, EdgeDirection, Graph, VertexId}
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext, graphx}

object GraphxHelloWorld extends App{

  //配置对象
  val conf = new SparkConf().setAppName("graphx").setMaster("local[3]")

  //创建sc对象
  val sc = new SparkContext(conf)
  //最短路径算法:计算的是从V1到所有顶点的最短路径
  val vertexRDD4:RDD[(VertexId,Int)] = sc.makeRDD(Array(
    (1L,0),
    (2L,Int.MaxValue),
    (3L,Int.MaxValue),
    (4L,Int.MaxValue),
    (5L,Int.MaxValue),
    (6L,Int.MaxValue),
    (7L,Int.MaxValue),
    (8L,Int.MaxValue),
    (9L,Int.MaxValue)
  ))
  val edgesRDD4 = sc.makeRDD(Array(
    Edge(1L,2L,6),
    Edge(1L,3L,3),
    Edge(1L,4L,1),
    Edge(3L,2L,2),
    Edge(3L,4L,2),
    Edge(2L,5L,1),
    Edge(5L,4L,6),
    Edge(5L,6L,4),
    Edge(6L,5L,10),
    Edge(5L,7L,3),
    Edge(5L,8L,6),
    Edge(4L,6L,10),
    Edge(6L,7L,2),
    Edge(7L,8L,4),
    Edge(9L,5L,2),
    Edge(9L,8L,3)
  ))

  val graph4 = Graph(vertexRDD4,edgesRDD4)
  val r = graph4.pregel[Int](
    //初始化消息的数据
    /*graph4.mapVertices((id,v)=>if(id == 1L) 0 else Int.MaxValue),*/
    //最大的迭代次数
    Int.MaxValue
    //激活态的消息发送的方向
    //EdgeDirection.Out
    )(
    //节点调用该消息将聚合后的数据和本节点进行属性的合并:求最小值
    (id,v,a) => math.min(v,a),
    //发送消息的方法
    triplet=>{
      //如果三元组的边的权重+入口的值小于目的的值，那么就发送消息，反之不发送
      if(triplet.srcAttr!= Int.MaxValue && triplet.srcAttr+triplet.attr<triplet.dstAttr){
        println(s"${triplet.srcAttr}--${triplet.attr}--${triplet.dstAttr}")
        Iterator((triplet.dstId,triplet.srcAttr+triplet.attr))
      }else{
        //不发送消息
        Iterator.empty
      }
    },
    //最后合并，取所有消息中的最小值
    (a,b) =>{
      println(s"merge:$a---$b")
      math.min(a,b)
    }
  )
  val r1 = r.triplets.collect()

  r1.foreach( triplet =>
    println(s"srcId=${triplet.srcId} srcAttr=${triplet.srcAttr}--edge=${triplet.attr}--dstId=${triplet.dstId} dstAttr=${triplet.dstAttr} ")
  )
  println(r.vertices.collect.mkString("\t"))

  sc.stop()



}

5. 应用

PageRank算法
(网页排名，Google左侧排名，佩奇排名)

1
2
3
4
5
6
7
8
9
10

-------------本文结束感谢您的阅读-------------